Note--National University of Singapore online course

lecture one

the main point is to introduces the basic aspects of the robotics.

core technology module

A. Mechanics

Familiarized with the fundamentals

• spatial representation, homogeneous transformations(齐次变换), forward and inverse kinematics(正运动学与逆运动学), velocity kinematics(速度运动学), Jacobian(雅可比行列式), static forces(静力)
• dynamics: Newtonian & Lagrangian formulation

B. Dynamics and control

Acquainted to the essentials

• feedback control(反馈控制), non-liner control, force control

C. Planning & Perception

Apply knowledge to topics in planning & perception

• path/ trajectory/ motion planning
• image formation, processing and analysis, visual tracking, vision-based control, image-guided robotics

the whole structure of the course and the knowledge

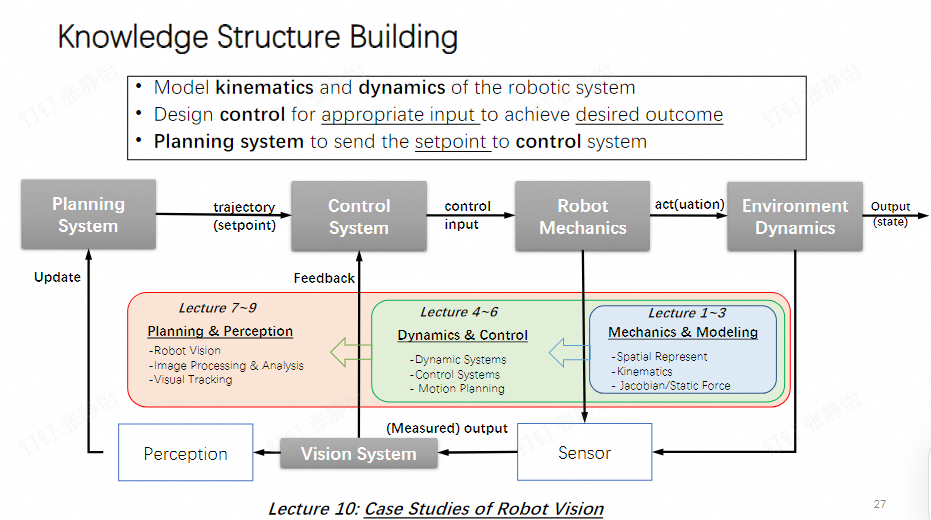we can have a glimpse of the whole sturcture from this picture

and this is the design process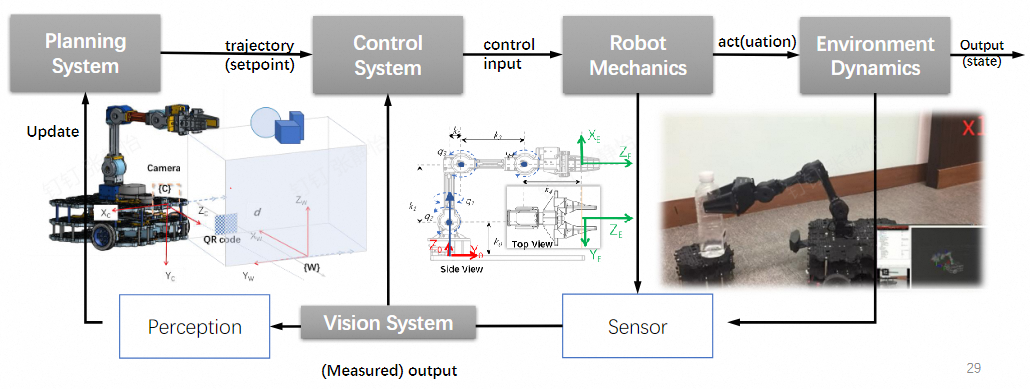

Mechanics

overview

kinematics(运动学)

The geometric description of motion, relating joint positions to end-effector pose without considering forces.

dynamics(动力学)

The study of forces/torques and their effects on robotic motion.

planning(规划)

The process of generating feasible paths or action sequences to achieve a task goal.

perception(感知)

Algorithms that interpret sensor data to model the environment and recognize objects.

control(控制)

Real-time algorithms that drive actuators to track planned trajectories while compensating for disturbances.

Spatial Representation & Transformation

Introduction to Robotics: Fundamentals

Coordinate Systems

Everyday-Examples of Coordinate Systems?

• On boardgames, on maps …… even the unit number on your address
• Can be 2D, (partial) 3D, Projective……

Homogenous Coordinate System 将3D点/向量升维到4D空间：

• 点的表示：(x, y, z) → (x, y, z, 1)

• 方向向量的表示：(x, y, z) → (x, y, z, 0)

关键：末尾的 1 或 0 成为区分点与向量的几何标签。

Reference Frames

• Frame is a coordinate system usually specified in position and orientation relative to other assigned coordinate systems
• Reference frames can be assigned to rigid bodies for the description of object poses and motions

Spatial Description Pose Representation (in ECE 470)

• Position and Orientation w.r.t a frame of reference
• Vector to represent position
• Matrix to represent orientation

for Matrix:

• 矩阵的列向量是单位向量（长度为1）
• 列向量之间相互正交（垂直）
• 满足正交矩阵特性

符号	含义
A_X_B	{B}的X轴在{A}系中的单位方向向量
A_Y_B	{B}的Y轴在{A}系中的单位方向向量
A_Z_B	{B}的Z轴在{A}系中的单位方向向量

✅ 应用示例：
当{B}是机器人末端坐标系，{A}是世界坐标系时：

• A_X_B 表示末端夹爪指向的方向
• A_Z_B 表示末端垂直于夹爪的方向

完整位姿 = 位置 + 方向 → 齐次变换矩阵 for check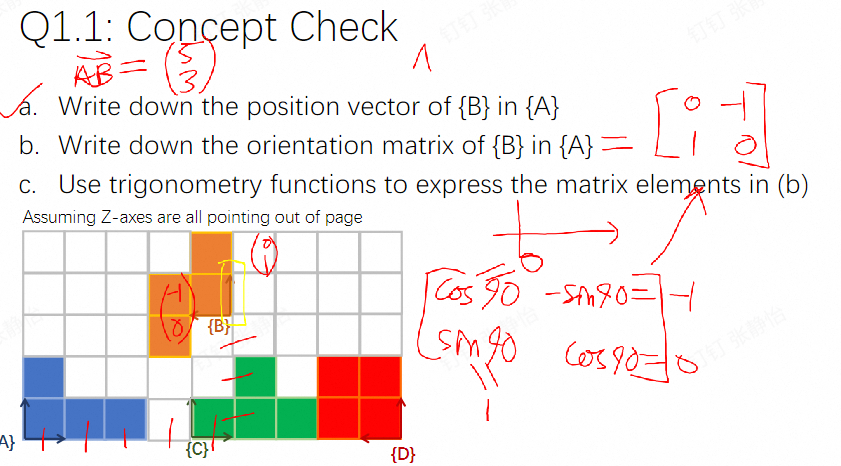

Lecture Two

Topics in Robotics

• Robot Kinematics
• Forward and Inverse Kinematics
• Homogeneous Transformations
• Denavit–Hartenberg Convention
• Velocity Kinematics

Coordinate Transformations & Homogeneous Representations

Spatial Relationships

• Robots operate in multiple coordinate frames
• Must convert between these using rotation + translation

2D Rotation Matrix

Given rotation angle $\theta$:

R(\theta) = \begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}

3D Rotation: Sequential Rotations

• Often decomposed into three elemental rotations: roll (x), pitch (y), yaw (z)
• Combined rotation matrix is their product in specified order

Homogeneous Transformation Matrix (HTM)

• Combines rotation and translation into one 4x4 matrix:

T = \begin{bmatrix}
R & p \\
0 & 1
\end{bmatrix}

Where:

• $R$: 3x3 rotation matrix
• $p$: 3x1 position vector

Composition:

T_{AC} = T_{AB} \cdot T_{BC}

Frame Interpretation

• Transformations can move vectors between frames
• Or describe frame poses relative to other frames

Forward Kinematics (FK)

Problem

Given joint angles $\theta_1, \theta_2, …, \theta_n$, find the pose of the end-effector

Approach

1. Assign coordinate frames using DH convention
2. Build each transformation $T_i$
3. Multiply them to obtain total transformation:

T = T_1 \cdot T_2 \cdot ... \cdot T_n

Properties of FK

• Deterministic: one unique pose per joint config
• Depends only on geometry and joint values

Denavit-Hartenberg (DH) Convention

Purpose

Standardize how coordinate frames are attached to links

DH Parameters (per joint i):

Parameter	Meaning
$\theta_i$	Joint angle (rotation about z)
$d_i$	Offset along z
$a_i$	Link length (along x)
$\alpha_i$	Twist angle (rotation about x)

DH Matrix Form

T_i = \begin{bmatrix}
\cos\theta_i & -\sin\theta_i\cos\alpha_i & \sin\theta_i\sin\alpha_i & a_i\cos\theta_i \\
\sin\theta_i & \cos\theta_i\cos\alpha_i & -\cos\theta_i\sin\alpha_i & a_i\sin\theta_i \\
0 & \sin\alpha_i & \cos\alpha_i & d_i \\
0 & 0 & 0 & 1
\end{bmatrix}

Example: 2-Link Planar Arm

• Link 1: length $L_1$, angle $\theta_1$
• Link 2: length $L_2$, angle $\theta_2$

Total HTM:

T = T_1(\theta_1) \cdot T_2(\theta_2)

Inverse Kinematics (IK)

Problem

Given end-effector pose $(x, y, \phi)$, find joint variables $\theta_i$

Challenges

• Multiple or infinite solutions
• May be no solution due to reachability limits
• Requires solving nonlinear equations

Example: 2-Link Planar Arm

x = L_1 \cos\theta_1 + L_2 \cos(\theta_1 + \theta_2) \\
y = L_1 \sin\theta_1 + L_2 \sin(\theta_1 + \theta_2)

Use geometric or algebraic techniques to isolate angles

Workspace & Reachability

Definitions

• Workspace: All positions reachable by the end-effector
• Dexterous workspace: Reachable with full orientation

Factors Affecting Workspace

• Link lengths, joint limits, singularities

Practice Problems

Q2.1: What is the workspace of a 2R planar manipulator?

Q2.3: Derive the DH matrix for a revolute joint with $\alpha = 0$, $a = L$, $d = 0$

Q2.5: Solve IK for 2R arm given $x = 1.5$, $y = 1.0$, $L_1 = L_2 = 1.0$

---

Lecture Three

Velocity Kinematics

What is Velocity Kinematics?

• Describes motion of robot links in terms of joint velocities
• Uses Jacobian matrix to relate joint velocity to end-effector linear/angular velocity

Twist Representation

• A 6D vector $\xi = [v; \omega]$ describes spatial velocity
• $v$: linear velocity
• $\omega$: angular velocity

Jacobian Matrix

\xi = J(q) \cdot \dot{q}

Where:

• $J$: Jacobian matrix (6×n)
• $q$: joint variables
• $\dot{q}$: joint velocities

Jacobian Columns

Each column corresponds to the contribution of one joint:

• Revolute joint:

\omega_i = z_i \\
v_i = z_i \times (p_e - p_i)

• Prismatic joint:

\omega_i = 0 \\
v_i = z_i

Jacobian Applications

Singularities

• Points where Jacobian loses rank
• Robot loses DOF in some direction

Velocity Mapping

• End-effector velocity in Cartesian space
• Useful for trajectory tracking, control

Static Force Mapping

• Transpose Jacobian maps Cartesian forces to joint torques:

\tau = J^T \cdot F

Practice Problems

Q3.1: Compute the Jacobian for a 2-link planar arm

Q3.2: Identify singular configurations for a 3R manipulator

Q3.3: Derive $\tau = J^T F$ for given external wrench

---

Lecture Four

Robot Dynamics

Newton-Euler Formulation

• Computes link accelerations, velocities, and forces
• Top-down (velocity) and bottom-up (force) recursion

Lagrangian Formulation

• Based on energy: $L = T - V$
• Apply Euler-Lagrange equations:

\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = \tau

General Form of Dynamics

M(q) \ddot{q} + C(q, \dot{q}) \dot{q} + g(q) = \tau

Where:

• $M(q)$: inertia matrix
• $C(q, \dot{q})$: Coriolis/centrifugal
• $g(q)$: gravity vector
• $\tau$: joint torques

Control

Position Control

\tau = K_p (q_d - q) + K_d (\dot{q}_d - \dot{q})

• PD control law
• Tracks desired trajectory

Force Control

• Useful in contact-rich tasks (e.g. polishing, assembly)
• Impedance control regulates dynamic interaction

Nonlinear Control

• Feedback linearization
• Adaptive control for unknown parameters

Practice Questions

Q4.1: Derive equations of motion for 2R robot using Lagrange method

Q4.2: Simulate PD control for setpoint tracking

Q4.3: Describe physical meaning of Coriolis term